
A motivação para esse artigo surgiu após uma longa jornada tentando estudar um ataque de bit flipping na cifra de modo CBC (Cipher Block Chaining). A conclusão da minha jornada inicial nesse estudo se deu após a construção de um desafio de CTF que eu criei para um evento da Boitatech. Esse artigo contemplará a teoria por trás do ataque.
English version: here
Primitivas
Antes de iniciar acredito que algumas leituras ou conhecimentos interessantes para acompanhar toda a lógica sejam as ideias gerais de criptografia, propriedades das operações XOR e claro, para a resolução dos exemplos, programação em Python.
Como descrito na wikipedia sobre modos de operação incluindo o CBC, eles garantem apenas a confidencialidade da mensagem, porém a intergidade é afetada. Isso é bem importante tendo em vista o ataque de bit-flipping que explora justamente essa propriedade.
AES CBC
O modo CBC é um dos modos de operação do AES (Advanced Encryption Standard) um algoritimo de criptografia simétrica, isso significa que a mesma chave é usada tanto para criptografar como descriptografar os dados.
Encryption
O CBC como o nome diz se refere a operação do algoritimo, que divide o plaintext em blocos, e cada bloco é sempre considerado na operação do bloco seguinte, a imagem a seguir mostra o processo.

Como o primeiro bloco não possui um bloco anterior, o que é usado é o Initialization Vector, mais conhecido como IV, então é feita uma operação XOR sendo o 1° bloco de plaintext $\oplus$ IV, o resultado é enviado para a função AES que resultará no primeiro bloco de ciphertext, note que esse bloco também vai para o XOR do segundo bloco de plaintext e assim o processo se repete com os demais blocos.
Na formula matematica:
\[\large C_i=E_k(P_i \oplus C_{i-1}) \\ \large C_0=IV\]Decryption

O processo de decrypt segue a lógica inversa do processo de encrypt, o primeiro bloco de ciphertext é utilizado na função de decrypt, e esse resultado é XOREADO com o IV para resultar no plaintext, note que no iníco, o primeiro bloco de ciphertext é jogado para a segunda etapa numa operação XOR com o resultado da função decrypt do segundo bloco. Assim o processo vai se repetindo sempre levando em consderação os blocos anteriores.
Na formula matemática:
\[\large P_i=D_k(C_i) \oplus C_{i-1} \\ \large C_0 = IV\]A exploração do bit-flipping que será abordada nos próximos tópicos ocorre por problemas na forma que o processo de Decrypt do CBC ocorre, entender ele é crucial para a execução do atque.
Bit flipping basics
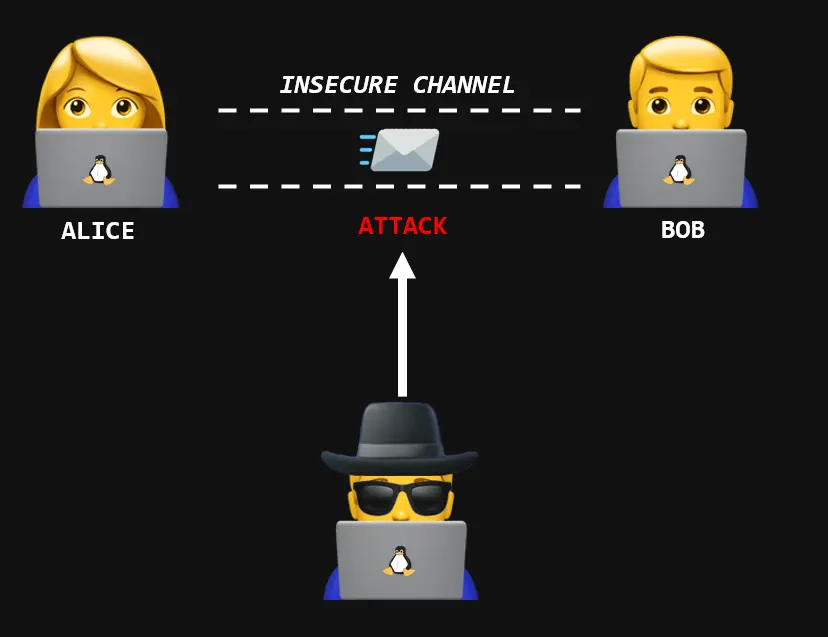
A ideia de bit-flipping pode ser explicada levando em consideração o cenário da imagem acima, em que existe um canal de comunicação inseguro. Para fins de exemplo levemos em consideração que a Alice enviará uma mensagem para Bob, essa mensagem será criptografada pela Alice portanto, o que será enviado mesmo será o ciphertext, Eve, o atacante interceptará o ciphertext no canal, e realizando o ataque de bit-flipping modificará o conteúdo do plaintext a partir do ciphertext sem conhecer a key, assim, Bob quando realizar o processo de decriptação após receber a mensagem terá um plaintext modificado. A confidencialidade da mensagem foi mantida, visto que ela continuou sendo criptografada e com o seu plaintext confidencial, porém a intergidade foi afetada visto que o plaintext foi alterado por Eve.
TLDR; bit-flipping é alterar o plaintext final
Acredito que as coisas ficarão mais claras durante a exploração e nos exemplos, mas tenha o TLDR em mente, o que estamos falando aqui é sobre modificar o conteúdo de mensagens sem conhecer a chave. Ao longo do artigo ficará claro que existem variações da exploração dependendo do quanto o atacante conhece do plaintext original e outros fatores relacionados a operação de criptografia em questão.
Understanding the problem
Como discutido anteriormente, o ataque de bit-flipping em CBC se dá por conta do processo de decrypt e tem relação com operações XOR.

Analisando a imagem acima temos:
- Processo de decrypt sendo realizado;
- Um plaintext/ciphertext de 3 blocos de 16 bytes,
3 * 16 bytes = 48 bytes no total
A fins de exemplo, vamos considerar o seguinte objetivo: Queremos alterar os terceiro, quarto e quinto bytes do terceiro bloco. No caso nós conhecemos o plaintext original.
Para isso será necessário modificar os terceiro, quarto e quinto bytes do segundo bloco. Pois perceba que eles fazem parte da operação XOR: $P_3 = D_k(C_3) \oplus C_2$, sendo:
- $P_3$ o plaintext do terceiro bloco;
- $C_2$ o ciphertext do segundo;
- $D_k(C_3)$ o resultado do decrypt do bloco 3;
O ataque de bit-flipping tem como objetivo alterar o plaintext final, no nosso caso o plaintext alterado será $P_3’$, para isso acontecer, deveremos alterar o ciphertext, no nosso caso o ciphertext do bloco anterior, chamaremos de $C_2’$, segue a lógica:
Acompanhe as operações a seguir:
- Começando com:
- Considerando um plaintext modificado teriamos:
- O fator comum entre as equações é $D_k(C_3)$, portanto substituindo na equação do plaintext modificado, temos:
Perceba como ficou a última equação, temos uma definição como sendo ciphertext modificado = plaintext original $\oplus$ ciphertext original anterior $\oplus$ plaintext que o atacante quiser. O mais interessante de tudo é que em nenhum momento precisamos da key ou entender as funções $E_k()$ e $D_k()$ conseguimos chegar a uma equação para realizar o ataque apenas com propriedades do XOR.
Equação geral do bit flipping:
\[\large P_i' = P_i \oplus C_{i-1} \oplus C_{i-1}' \\ \large C_{i-1}' = P_i \oplus C_{i-1} \oplus P_i' \\ \large C_0 = IV ^ * \\ \large C_0' = IV' ^ *\]- * : É possível também trabalhar com o IV dependendo do caso, no exemplo do desafio de CTF abordado nesse artigo o ataque envolve modificação do IV
Weponazing
Agora que possuimos uma definição teórica sobre o ataque e o modo de operação CBC, vamos aos exemplos práticos. Para facilitar algumas coisas, usaremos duas bibliotecas do python:
$ pip install pycryptodome pwntools
Iniciaremos o seguinte script para gerar o ciphertext que iremos atacar:
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad, unpad
def encrypt(key, iv, plaintext):
plaintext = pad(plaintext.encode(), AES.block_size)
# add padding
cipher = AES.new(key, AES.MODE_CBC, iv)
ciphertext = cipher.encrypt(plaintext)
return ciphertext
# random generated 16 bytes key
key = bytes.fromhex('63f835d0e3b9c70130797be59e25c00f')
# random generated 16 bytes iv
iv = bytes.fromhex('b05fee43fe4db7c5503b1f6732fedd1b')
print('Key: ', key.hex())
print('IV: ', iv.hex())
plaintext = 'DOGECOIN transaction: 100 DOGE to [email protected]'
print('Plaintext: ', plaintext)
ciphertext = encrypt(key, iv, plaintext)
print('Ciphertext in bytes:', ciphertext)
print('Ciphertext in hex: ', ciphertext.hex())
Note que o plaintext do exemplo é:
plaintext = 'DOGECOIN transaction: 100 DOGE to [email protected]'
Agora vamos ao cenário do ataque:
Alice realiza uma transação DOGECOIN e envia 100 DOGE para BOB, que possuí o endereço “[email protected]”. Eve, o atacante pretende realizar um ataque de bitflipping e alterar o destino dos bitcoins para “[email protected]”.
Com o cenário do ataque em mente, podemos montar então o plaintext modificado e traçar nossos bytes “alvos”.
mod_plaintext = 'DOGECOIN transaction: 100 DOGE to [email protected]'
# ^^^
Nesse exemplo prático coloquei os bytes a serem alterados na mesma posição do exemplo teórico buscando um melhor entendimento. Perceba que a diferença entre o plaintext original e o modificado são apenas o terceiro, quarto e quinto byte do terceiro bloco, então temos:
- B vira E (terceiro byte do terceiro bloco, 34° do total)
- O vira V (quarto byte do terceiro bloco, 35° do total)
- B vira E (quinto byte do terceiro bloco, 36° do total)
Lembrando a equação do bit-flipping apresentada em tópicos anteriores:
\[\large C_{i-1}' = P_i \oplus C_{i-1} \oplus P_i'\]Buscando transformar da matemática para o Python, precisamos nos atentar que na formula matemática estamos nos referindo aos blocos de ciphertext/plaintext, onde $i$ representa o número do bloco, quando pensamos em Python, está sendo realizado uma operação “byte a byte”, estamos nos referindo exatamente a posição do byte que queremos modificar em relação ao ciphertext/plaintext, portanto aplicando isso, $i$ agora será a posição do byte a ser modificado no plaintext final, agora teremos que buscar essa mesma posição mas relacionada ao bloco anterior, ou seja, voltando 16 bytes para trás, logo $C_{i-1}’$ seria em python mod_ciphertext[i - 16].
target_pos = i
mod_ciphertext[i - 16] = plaintext[i] ^ ciphertext[i - 16] ^ mod_plaintext[i]
# mod_ciphertext = original_byte_plaintext ^ original_ciphertext_in_previous_block ^ malicious_mod_plaintext_byte
Perceba, é uma operação relacionada diretamente aos bytes! Caso você esteja buscando uma operação em python que defina todo esse artigo, está logo acima, se é pra lembrar de algo lembre dela!
Bit-flipping attack
Para aplicar essa operação no script e realizar o ataque, precisamos modificar um pouco o código, adicionando uma função de decrypt (para testar se o ataque funcionou). Note que existe uma key no código, mas apenas para criar o ciphertext e depois realizar o decrypt, ela não é usada no ataque.
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad, unpad
def encrypt(key, iv, plaintext):
plaintext = pad(plaintext.encode(), AES.block_size)
# add padding
cipher = AES.new(key, AES.MODE_CBC, iv)
ciphertext = cipher.encrypt(plaintext)
return ciphertext
def decrypt(key, iv, ciphertext):
cipher = AES.new(key, AES.MODE_CBC, iv)
plaintext = cipher.decrypt(ciphertext)
plaintext = unpad(plaintext, 16)
# remove padding
return plaintext
key = bytes.fromhex('63f835d0e3b9c70130797be59e25c00f')
iv = bytes.fromhex('b05fee43fe4db7c5503b1f6732fedd1b')
plaintext = 'DOGECOIN transaction: 100 DOGE to [email protected]'
original_plaintext = plaintext
ciphertext = encrypt(key, iv, plaintext)
mod_plaintext = 'DOGECOIN transaction: 100 DOGE to [email protected]'
target_pos1 = 34 # B to E
target_pos2 = 35 # O to V
target_pos3 = 36 # B to E
mod_ciphertext = bytearray(ciphertext)
# change B to E in position 34
mod_ciphertext[target_pos1 - 16] = ord('B') ^ ciphertext[target_pos1 - 16] ^ ord('E') # xor operation
# change O to V in position 35
mod_ciphertext[target_pos2 - 16] = ord('O') ^ ciphertext[target_pos2 - 16] ^ ord('V') # xor operation
# change B to E in position 36
mod_ciphertext[target_pos3 - 16] = ord('B') ^ ciphertext[target_pos3 - 16] ^ ord('E') # xor operation
print('[+] Old ciphertext: ', ciphertext.hex())
print('[+] New ciphertext: ', mod_ciphertext.hex())
print('[-] Decrypting...')
mod_plaintext = decrypt(key, iv, mod_ciphertext)
print('[+] Original plaintext: ', original_plaintext)
print('[+] Modified ciphertext ', mod_plaintext)
E de resultado temos:

b'DOGECOIN transac\xc9L\xba\xf3l\xdatY\xb4\x94\xcd{\xef%+po [email protected]'
Conseguimos alterar o plaintext! O nosso ciphertext malicioso e modificado entrou no decrypt e no final obtivemos o plaintext modificado! Por si só, o ataque foi concluido, mas como pode ser percebido, o plaintext final ficou com certos bytes estranhos, que não condizem com o plaintext original.
Variations
Antes de iniciar o tópico de variações do ataque, gostaria de trazer novamente a imagem que representa o ataque de bit-flipping.

Perceba as cores e idendifique-as no print do terminal que contém o resultado do ataque.
- Amarelo: Os bytes modificados do ciphertext
- Verde: O plaintext modificado
- Vermelho: Os bytes correspondentes do bloco anterior aos bytes do plaintext modificado; o bloco inteiro foi prejudicado, afetando o plaintext final.
A conclusão em relação a parte de cor vermelha é: Como o ciphertext foi alterado para modificação do plaintext, esse bloco alterado do ciphertext, quando passar pela função de decrypt resultará em um bloco plaintext diferente e alterado.
Recursively in each block
O pensamento que o atacante deverá ter nessa hora é um pensamento ligado a recursividade, agora temos um ciphertext modificado, que produz um plaintext com um endereço de e-mail malicioso (EVE), porém esse plaintext possui bytes errados no meio dele. Pois então, com isso temos a mesma situação do ínicio, Um plaintext que conhecemos que precisa ser alterado (alterar os bytes que sairam errado para os bytes certos que conhecemos do plaintext)…
No primeiro exemplo, o ataque foi realizado em cada byte, “linha por linha” no python, mas o ideal seria uma função genérica que fizesse o ataque. Portanto, aqui se inicia a fase do desenvolvimento do algoritimo para realizar ataques de bit-flipping em CBC automaticamente.
É claro que isso dependeria do atacante ter acesso ao resultado inteiro do plaintext final, sem isso, é impossível seguir os próximos passos. Ou seja, de alguma forma o atacante tem que ser capaz de enviar um ciphertext e obter o resultado do decrypt desse ciphertext.
Exploit
Para iniciar a automação do ataque, primeiro é necessário encontrar uma forma de encontrar as diferenças entre um conjunto de bytes e outro, no nosso caso, entre o plaintext original e o modificado, encontrando essas diferenças, as posições de cada byte a ser modificado devem ser guardadas.
Basicamente o que faremos é um diff, e o que usaremos será uma das propriedades do XOR:
\[\large A \oplus A = 0 \\ \large A \oplus B \ne 0\]Algo XOREADO com ele mesmo é sempre Null, se for algo diferente dele mesmo, sempre resulta em algo diferente, tente executar o script a seguir:
from termcolor import colored
from pwn import xor
def bit_flipping(original_plaintext: bytes, modified_plaintext: bytes):
diff_positions = []
for position, byte_ in enumerate(original_plaintext):
x = xor(original_plaintext[position], modified_plaintext[position]) # xor each byte
if x != b'\x00': # if the result is not null, then it is different
diff_positions.append(position)
# just to visualize what is happening in colors, ignore
og = ''
for i, b in enumerate(original_plaintext):
if i in diff_positions:
og += colored(chr(b), 'red')
else:
og += chr(b)
mod = ''
for i, byte_ in enumerate(modified_plaintext):
if i in diff_positions:
mod += colored(chr(byte_), 'green')
else:
mod += chr(byte_)
print('[+] Original plaintext: ', og)
print('[+] Modified plaintext: ', mod)
print('[+] Positions to be modified: ', diff_positions)
Output:

Agora temos uma forma de saber o que deve ser alterado e o que deve ser mantido. Seguindo a lógica desenvolvida, vamos adicionar no código um algoritimo para alterar cada um desses bytes de plaintext nessas posições alterando o ciphertext nessas posições - 16.
OBS: Talvez você tenha pensado: “Mas e as posições a serem alteradas que forem menores que 16?”. Para essas posições teríamos que alterar o IV, vamos trabalhar com isso mais tarde, portando, por enquanto vamos pegar apenas as posições que forem >= que 16.
def bit_flipping(original_plaintext: bytes, modified_plaintext: bytes, ciphertext: bytes):
diff_positions = []
for position, byte_ in enumerate(original_plaintext):
x = xor(original_plaintext[position], modified_plaintext[position]) # xor each byte
if x != b'\x00': # if the result is not null, then it is different
diff_positions.append(position)
ciphertext = list(ciphertext)
diff_positions.reverse()
diff_positions = [position for position in diff_positions if position >= 16]
for position in diff_positions:
ciphertext[position - 16] = original_plaintext[position] ^ ciphertext[position - 16] ^ modified_plaintext[position]
ciphertext = bytes(ciphertext)
return ciphertext
original_plaintext = b'DOGECOIN transaction: 100 DOGE to [email protected]'
mod_plaintext = b'DOGECOIN transaction: 100 DOGE to [email protected]'
ciphertext = encrypt(key, iv, original_plaintext)
new_ciphertext = bit_flipping(original_plaintext, mod_plaintext, ciphertext)
print(decrypt(key, iv, new_ciphertext))
A função pega posições e altera o ciphertext do bloco anterior usando a fórmula $C_{i-1}’= P_i \oplus C_{i-1} \oplus P_i’$ (linha 13), e ao final retorna o ciphertext.
Executando temos como output:
b'DOGECOIN transac\xc9L\xba\xf3l\xdatY\xb4\x94\xcd{\xef%+po [email protected]'
Exatamente o que tinhamos antes, agora para brincar mais um pouco, experimente alterar mais coisas do último bloco do plaintext, usando um mod_plaintext = b'DOGECOIN transaction: 100 DOGE to [email protected]' (alterando do dominio do e-mail) temos:
b'DOGECOIN transac]p\xc7P\xb6?)\xb6\xbb\x8av\x8c\xb68\x01\xe9o [email protected]'. Pode ver que foi alterado.
Agora temos uma parte do exploit, uma função capaz de identificar os bytes a serem alterados e realizar o ataque de forma automática, mas ainda temos alguns problemas, o plaintext final ainda fica errado, agora sim vamos aplicar a recursividade que foi falada nos tópicos anteriores.
def bit_flipping(original_plaintext: bytes, modified_plaintext: bytes, ciphertext: bytes):
diff_positions = []
for position, byte_ in enumerate(original_plaintext):
x = xor(original_plaintext[position], modified_plaintext[position]) # xor each byte
if x != b'\x00': # if the result is not null, then it is different
diff_positions.append(position)
ciphertext = list(ciphertext)
diff_positions.reverse()
diff_positions = [position for position in diff_positions if position >= 16]
for position in diff_positions:
ciphertext[position - 16] = original_plaintext[position] ^ ciphertext[position - 16] ^ modified_plaintext[position]
ciphertext = bytes(ciphertext) # this ciphertext is wrong
# recursively call the function until the modified plaintext is equal to the plaintext
mod_final_plaintext = decrypt(key, IV, ciphertext) # the attacker needs to be able to decrypt the ciphertext
new_ciphertext = ciphertext ## need to change the ciphertext again
while mod_final_plaintext[16:] != modified_plaintext[16:]:
new_ciphertext = bit_flipping(mod_final_plaintext, modified_plaintext, new_ciphertext)
mod_final_plaintext = decrypt(key, IV, new_ciphertext)
return new_ciphertext
Para usar a recursividade ao nosso favor, o que o algoritimo faz é encarar o ciphertext modificado que gera o plaintext estranho, como um novo ciphertext a ser modificado, então rodamos recursivamente a função (linha 22) usando como alvo o new_ciphertext (esse ciphertext que gera o plaintext errado). Note que ainda no while é pego apenas do 16 byte para frente, isso pois ainda não começamos a mexer no IV.
Após executar temos:
b'\xc6\xd1\xad=\xabF\xd6\xcbE\r\x0b\xfe\xa8\x0b<Ftion: 100 DOGE to [email protected]'
Deu certo! Agora o segundo bloco que estava vindo errado ja aparece, para brincar um pouco podemos modificar por exemplo o valor da transação para 999. Rodando temos:
b'\x08\xd4\xf1\x92\x90\x16\xd4\x07\x8c\xaa\xc4\xc9\x9c\xad\xd28tion: 999 DOGE to [email protected]'
Note que ainda temos um plaintext final que tem bytes errados, os pertencentes ao primeiro bloco, como arrumar? Para isso teremos que entrar em uma variação do ataque de bitflipping, a que o atacante consegue modificar o IV utilizado na função de decrypt. Alterando o IV, poderemos arrumar o primeiro bloco, e assim teremos um plaintext 100% limpo.
E como alterar o IV? Usando a equação geral chegamos em:
\[\large C_{1-1}' = C_0' = IV' = P_1 \oplus IV \oplus P_1' \\ \large C_0 = IV\]A fim de aplicar isso no nosso algoritimo temos que modificar nossa função adicionando dois novos argumentos, o changeiv e o iv.
def bit_flipping(original_plaintext: bytes, modified_plaintext: bytes, ciphertext: bytes, changeiv=False, iv=None):
diff_positions = []
for position, byte_ in enumerate(original_plaintext):
x = xor(original_plaintext[position], modified_plaintext[position]) # xor each byte
if x != b'\x00': # if the result is not null, then it is different
diff_positions.append(position)
ciphertext = list(ciphertext)
diff_positions.reverse()
diff_positions = [position for position in diff_positions if position >= 16]
for position in diff_positions:
ciphertext[position - 16] = original_plaintext[position] ^ ciphertext[position - 16] ^ modified_plaintext[position]
ciphertext = bytes(ciphertext) # this ciphertext is wrong
# recursively call the function until the modified plaintext is equal to the plaintext
mod_final_plaintext = decrypt(key, IV, ciphertext) # the attacker needs to be able to decrypt the ciphertext
new_ciphertext = ciphertext ## need to change the ciphertext again
while mod_final_plaintext[16:] != modified_plaintext[16:]:
new_ciphertext = bit_flipping(mod_final_plaintext, modified_plaintext, new_ciphertext)
mod_final_plaintext = decrypt(key, IV, new_ciphertext)
if changeiv == True:
# the firts 16 bytes of our modified plaintext are wrong, so we need to change the iv, lets get exactly the first 16 bytes wrongs positions of the plaintext
# like diff again
wrong_positions = []
for position, byte_ in enumerate(mod_final_plaintext[:16]):
x = xor(mod_final_plaintext[position], modified_plaintext[position])
if x != b'\x00':
wrong_positions.append(position)
# iv to change
new_iv = list(iv)
for wrong_position in wrong_positions:
new_iv[wrong_position] = mod_final_plaintext[wrong_position] ^ iv[wrong_position] ^ modified_plaintext[wrong_position]
new_iv = bytes(new_iv)
# return a tuple contaning the new ciphertext and the new iv
return new_ciphertext, new_iv
return new_ciphertext
original_plaintext = b'DOGECOIN transaction: 100 DOGE to [email protected]'
mod_plaintext = b'DOGECOIN transaction: 999 DOGE to [email protected]'
ciphertext = encrypt(key, iv, original_plaintext)
new_ciphertext, new_iv = bit_flipping(original_plaintext, mod_plaintext, ciphertext, changeiv=True, iv=iv)
print(decrypt(key, new_iv, new_ciphertext))
Ao checar se é necessário mudar o iv (linha 26), primeiro é executado a parte do diff, para conseguir as posições exatas do que deve ser mudado, a aplicação da equação ocorre na linha 38, onde o new_iv é modificado utilizando a equação. Note que não é utilizado algo como position - 16, isso por que o IV é outra coisa, a parte do ciphertext, o que fazemos é apenas refletir a posição para ele, ja que ambos o primeiro bloco do ciphertext e o IV possuem 16 byres de tamanho.
Após a execução temos como resultado: b'DOGECOIN transaction: 999 DOGE to [email protected]'
Agora sim, um plaintext final perfeito! Como de costume, para brincar, experimente mudar o mod_plaintext para apenas espaços vazios…
original_plaintext = b'DOGECOIN transaction: 100 DOGE to [email protected]'
mod_plaintext = b' '
ciphertext = encrypt(key, iv, original_plaintext)
new_ciphertext, new_iv = bit_flipping(original_plaintext, mod_plaintext, ciphertext, changeiv=True, iv=iv)
print(decrypt(key, new_iv, new_ciphertext))
Executando…

Da certo também, isso prova que agora é possível fazer qualquer tipo de alteração.
Conclusion
Após algumas pesquisas, não encontrei muitos ataques ou vulnerabilidades que envolvam especificamente bit-flipping em CBC, acredito que até então se trate de uma vulnerabilidade teórica, que normalmente é encontrada em desafios de CTF de criptografia. Encontrei dificuldade em pesquisar sobre o tema pela complexidade dele, e pelo fato de muitos artigos estarem focados em desafios de CTF especificos, então decidi escrever esse artigo para abordar o tema de forma geral, sem desafios de CTF envolvidos, trazer a teoria e as operações matemáticas buscando abordar um exemplo e carrega-lô até o final com o objetivo de construir um algoritimo/exploit genérico para qualquer situação (dentro das variações do ataque).
É importante ressaltar que esse artigo foi construido a partir de uma pesquisa e estudo pessoal, portanto, pode conter erros, caso encontre algum, por favor, me avise para que eu possa corrigir. Caso isso aconteça, mande um e-mail para: [email protected] ou abra uma issue no repositório desse blog.
Obrigado por ler!